BPE 13 Einheitsübergreifend
1 Uneigentliches Integral (40 min) 𝕃
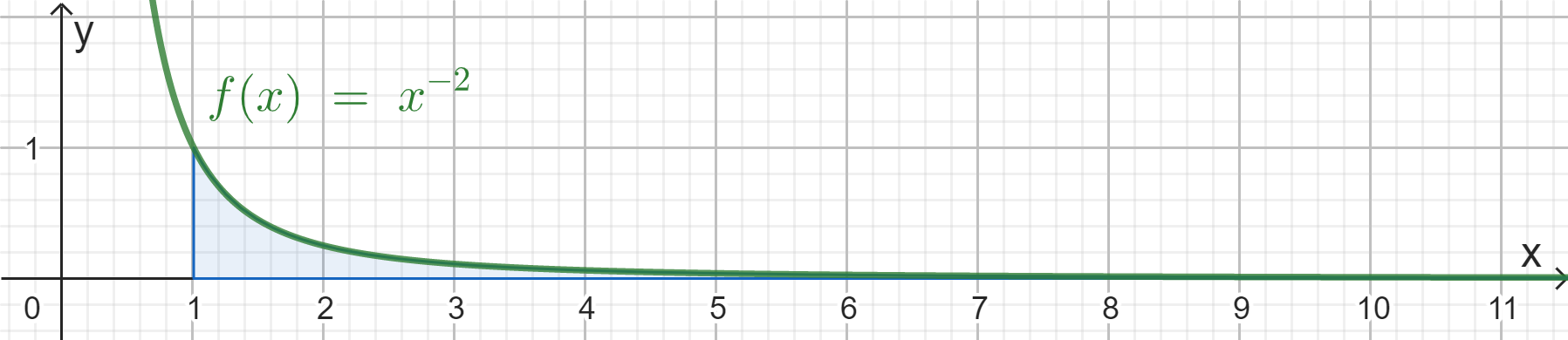
Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit \(p(x)=x^q;\: x\neq 0\).
Für \(b \rightarrow \infty\) heißt \(U_q=\int_1^b{p(x)}\cdot dx\) uneigentliches Integral über p, falls \(U_q\) eine reelle Zahl ergibt.
Überprüfe, für welche Werte von q das uneigentliche Integral \(U_q\) existiert.
| AFB III - K2 K5 | Quelle Dr. Andreas Dinh | #problemlösen |
2 Annäherung (30 min) 𝕃
 In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
- Bestimme a in Abhängigkeit von q.
Begründe, weshalb ein kleiner Wert des Integrals
\[\int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx\]ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.
- Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.
(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)
| AFB III - K2 K5 K4 | Quelle Dr. Andreas Dinh | #problemlösen |
3 Steigung, Volumen (k.A.) 𝕃
Die Abbildung zeigt den Graphen einer in \(\mathbb{R}\) definierten Funktion \(f\).
- Beurteile die folgende Aussage:
Für jeden Wert von \(x\) mit \(0\leq x\leq 2\) ist die Steigung des Graphen von \(f\) kleiner als 3. - Mit dem Term \(\pi\cdot\int\limits_{0}^{2}{\left(f\left(x\right)\right)^2\mathrm{d} x}\)
kann das Volumen eines Körpers berechnet werden.
Begründe, dass dieses Volumen größer als \(\pi\cdot{0,5}^2+\pi\cdot1^2\) ist.
| AFB k.A. - K1 K2 K4 K5 K6 | Quelle IQB e.V. | #iqb |
4 Stau MMS (k.A.) 𝕃
- Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau.
An einem bestimmten Tag entsteht der Stau um 06:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge mithilfe der in \(\mathbb{R}\) definierten Funktion \(f\) mit \(f\left(x\right)=x\cdot\left(8-5x\right)\cdot\left(1-\frac{x}{4}\right)^2\) beschrieben werden. Dabei gibt \(x\) die nach 06:00 Uhr vergangene Zeit in Stunden und \(f\left(x\right)\) die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
- Nenne die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründe anhand der Struktur des Funktionsterms von f, dass es keine weiteren solchen Zeitpunkte gibt.
- Es gilt \(f\left(2\right)<0\). Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
- Bestimme den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt. Zeige, dass der zugehörige Wert der momentanen Änderungsrate zwischen 2 km/h und 3 km/h liegt.
- Gib den Zeitpunkt an, zu dem der Stau am längsten ist. Begründe deine Angabe.
Im Sachzusammenhang ist neben der Funktion \(f\) die in \(\mathbb{R}\) definierte Funktion \(s\) mit \(s\left(x\right)=\left(\frac{x}{4}\right)^2\cdot\left(4-x\right)^3\) von Bedeutung.
- Begründe, dass die folgende Aussage richtig ist:
Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion \(s\) angegeben werden.
Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat. - Berechne die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimme für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge.
- Bestimme denjenigen Zeitpunkt zwischen 06:00 Uhr und 10:00 Uhr, zu dem
die Staulänge 0,5 km geringer ist als eine Stunde vorher.
- Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 1 gezeigten Graphen dargestellt. Dabei ist x die nach 06:00 Uhr vergangene Zeit in Stunden und y die momentane Änderungsrate der Staulänge in Kilometer pro Stunde.
Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat. Markiere diesen Zeitpunkt in der Abbildung 1, begründe deine Markierung und veranschauliche deine Begründung in der Abbildung 1.
- Betrachtet wird die Schar der in \(\mathbb{R}\) definierten Funktionen \(h_k\) mit \(h_k\left(x\right)=\left(x-3\right)^k+1\) und \(k\in\mathbb{N}\setminus\left\{0\right\}\).
- Das Verhalten von \(h_k\) für \(x\rightarrow-\infty\) ist abhängig von \(k\). Gib die dabei auftretenden Fälle des Verhaltens und für diese Fälle jeweils einen passenden Wert von \(k\) an. Begründe jeweils die Angabe des Werts von \(k\).
- Ermittle die Koordinaten derjenigen Punkte, die alle Graphen der Schar gemeinsam haben.
- Die erste Ableitungsfunktion von \(h_k\) wird mit \(h_k^\prime\) bezeichnet. Beurteile die folgende Aussage:
Es gibt genau einen Wert von \(k\), für den der Graph von \(h_k^\prime\) Tangente an den Graphen von \(h_k\) ist. - Die Graphen von \(h_k\) und \(h_k^\prime\) werden in der Abbildung 2 für \(k=4\) beispielhaft für gerade Werte von \(k\) gezeigt, in der Abbildung 3 für \(k=5\) beispielhaft für ungerade Werte von \(k\).
Für \(k\geq4\) werden die Punkte \(P\left(4\middle| h_k\left(4\right)\right),Q\left(4\middle| h_k^\prime\left(4\right)\right),R\left(2\middle| h_k\left(2\right)\right)\) und \(S\left(2\middle| h_k^\prime\left(2\right)\right)\) betrachtet. Diese Punkte sind jeweils Eckpunkte eines Vierecks. Begründe, dass jedes dieser Vierecke ein Trapez ist, und zeige, dass die folgende Aussage richtig ist:
Für jeden geraden Wert von von \(k\) mit \(k\geq4\) stimmen der Flächeninhalt des Trapezes für \(k\) und der Flächeninhalt des Trapezes für \(k+1\) überein.
| AFB I, II, III - K1 K2 K3 K4 K5 K6 | Quelle IQB e.V. | #iqb |
5 Stau WTR (k.A.) 𝕃

Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau.
An einem bestimmten Tag entsteht der Stau um 06:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge mithilfe der in \(\mathbb{R}\) definierten Funktion \(f\) mit
beschrieben werden. Dabei gibt \(x\) die nach 06:00 Uhr vergangene Zeit in Stunden und \(f\left(x\right)\) die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
Die Abbildung 1 zeigt den Graphen von \(f\) für \(0\le x\le4\).
Für die erste Ableitungsfunktion von \(f\) gilt \(f^\prime\left(x\right)=\left(5x^2-16x+8\right)\cdot\left(1-\frac{x}{4}\right)\).
- Nenne die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründe anhand der Struktur des Funktionsterms von \(f\), dass es keine weiteren solchen Zeitpunkte gibt.
- Es gilt \(f\left(2\right)<0\). Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
- Bestimme rechnerisch den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt.
- Gib den Zeitpunkt an, zu dem der Stau am längsten ist. Begründe deine Angabe.
Im Sachzusammenhang ist neben der Funktion \(f\) die in \(\mathbb{R}\) definierte Funktion \(s\) mit \(s\left(x\right)=\left(\frac{x}{4}\right)^2\cdot\left(4-x\right)^3=-\frac{1}{16}x^5+\frac{3}{4}x^4-3x^3+4x^2\) von Bedeutung.
- Begründe, dass die folgende Aussage richtig ist:
Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion \(s\) angegeben werden.
Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat. - Berechne die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimme für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge.

- Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 2 gezeigten Graphen dargestellt. Dabei ist x die nach 06:00 Uhr vergangene Zeit in Stunden und y die momentane Änderungsrate der Staulänge in Kilometer pro Stunde.
Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat. Markiere diesen Zeitpunkt in der Abbildung 2, begründe deine Markierung und veranschauliche deine Begründung in der Abbildung 2.
2. Betrachtet wird die Schar der in \(\mathbb{R}\) definierten Funktionen \(h_k\) mit \(h_k\left(x\right)=\left(x-3\right)^k+1\) und \(k\in\mathbb{N}\setminus\left\{0\right\}\).
- Gib in Abhängigkeit von \(k\) das Verhalten von \(h_k\) für \(x\rightarrow-\infty\) an und begründe deine Angabe.
- Ermittle die Koordinaten der beiden Punkte, die alle Graphen der Schar gemeinsam haben.
- Die erste Ableitungsfunktion von \(h_k\) wird mit \(h_k^\prime\) bezeichnet. Beurteile die folgende Aussage:
Es gibt genau einen Wert von \(k\), für den der Graph von \(h_k^\prime\) Tangente an den Graphen von \(h_k\) ist. - Die Graphen von \(h_k\) und \(h_k^\prime\) werden in der Abbildung 3 für \(k=4\) beispielhaft für gerade Werte von \(k\) gezeigt, in der Abbildung 4 für \(k=5\) beispielhaft für ungerade Werte von \(k\).

Für \(k\geq4\) werden die Punkte \(P\left(4\middle| h_k\left(4\right)\right),Q\left(4\middle| h_k^\prime\left(4\right)\right),R\left(2\middle| h_k\left(2\right)\right)\) und \(S\left(2\middle| h_k^\prime\left(2\right)\right)\) betrachtet. Diese Punkte sind jeweils Eckpunkte eines Vierecks. Begründe, dass jedes dieser Vierecke ein Trapez ist, und zeige, dass die folgende Aussage richtig ist:
Für jeden geraden Wert von von \(k\) mit \(k\geq4\) stimmen der Flächeninhalt des Trapezes für \(k\) und der Flächeninhalt des Trapezes für \(k+1\) überein.
| AFB I, II, III - K1 K2 K3 K4 K5 K6 | Quelle IQB e.V. | #iqb |
6 Schalldruck1 (k.A.) 𝕃

Gegeben ist die Schar der in \(\mathbb{R}\) definierten Funktionen \(f_a:\ x\mapsto e^x\cdot\left(x-a\right)^2\) mit \(a\in\mathbb{R}\). Der Graph von \(f_a\) wird mit \(G_a\) bezeichnet. Jeder Graph der Schar hat genau einen Hochpunkt und genau einen Tiefpunkt. Die Abbildung 1 zeigt \(G_\frac{3}{2}\).
- \(G_\frac{3}{2}\) nimmt in einem seiner Wendepunkte seine kleinste Steigung an. Bestimme diese Steigung rechnerisch.
- \(G_a\) hat mit jeder der beiden Koordinatenachsen genau einen gemeinsamen Punkt. Gib die Koordinaten dieser Punkte an und begründe, dass der gemeinsame Punkt mit der x-Achse der Tiefpunkt von \(G_a\) ist.
- Es gibt einen positiven Wert von \(a\), für den \(G_a\) und die Koordinatenachsen eine Fläche mit dem Inhalt 3 einschließen. Bestimme diesen Wert von \(a\).
- Für jeden Wert von \(a\) mit \(a\neq0\) schließt die Gerade durch die beiden Extrempunkte von \(G_a\) mit den Koordinatenachsen ein Dreieck ein. Berechne denjenigen Wert von \(a\), für den dieses Dreieck gleichschenklig ist.
Betrachtet werden die in \(\mathbb{R}\) definierten Funktionen \(f_{a,b}:\ x\mapsto e^x\cdot\left(\left(x-a+b\right)^2-b\right)\) mit \(a,b\in\mathbb{R}\). Es gilt \(f_{a,0}\left(x\right)=f_a\left(x\right)\). Der Graph von \(f_{a,b}\)wird mit \(G_{a,b}\) bezeichnet.
- Für positive Werte von \(b\) hat \(G_{a,b}\) zwei Schnittpunkte mit der x-Achse. Für jeden Wert von \(a\) wird der Abstand dieser beiden Schnittpunkte betrachtet. Zeige rechnerisch, dass dieser Abstand unabhängig von \(a\) ist.
Erhöht man im Term von \(f_{a,b}\) den Wert von \(b\) um 1, so erhält man einen Term der ersten Ableitungsfunktion von \(f_{a,b}\). Es gilt also \(f_{a,b}^\prime\left(x\right)=f_{a,b+1}\left(x\right)\).
- Die Abbildung 2 zeigt für einen bestimmten Wert von \(a\) die Graphen zweier Funktionen der Schar, bei denen sich die Werte von \(b\) um 1 unterscheiden. Entscheide, welcher der beiden Graphen I und II zum größeren Wert von \(b\) gehört, und begründe deine Entscheidung.

- Für jeden Wert von \(a\) gilt \(f_{a,0}\left(a\right)=0\ \land\ f_{a,1}\left(a\right)=0\ \land\ f_{a,2}\left(a\right)\neq0\). Gib die Bedeutung dieser Tatsache für die Graphen der Funktion \(f_{a,-1}\) an.
| AFB I, II, III - K1 K2 K4 K5 K6 | Quelle IQB e.V. | #iqb |
7 Schalldruck2 (k.A.) 𝕃
Der Schalldruckpegel eines bestimmten Wecktons wird durch die in \(\left[0;4\right]\) definierte Funktion
beschrieben. Dabei ist \(x\) die seit Beginn des Wecktons vergangene Zeit in Sekunden und \(h\left(x\right)\) der Schalldruckpegel in Dezibel (dB). Die Abbildung 3 zeigt einen Teil des Graphen von \(h\).
- Zeige, dass der Graph von \(h\) bei \(x=2\) keinen Sprung aufweist, und vervollständige den Graphen von \(h\) in der Abbildung 3.
- Berechne den Zeitpunkt, zu dem der Weckton den größten Schalldruckpegel hat, und gib diesen Schalldruckpegel an.
- Berechne unter Verwendung der folgenden Information den durchschnittlichen Funktionswert von \(h\).
Der durchschnittliche Funktionswert von \(h\) im Intervall \(\left[a;b\right]\) stimmt mit der Höhe eines Rechtecks überein, das die beiden folgenden Eigenschaften hat:
• Das Rechteck hat die Breite \(b-a\).
• Das Rechteck hat den gleichen Inhalt wie die Fläche, die für \(a\le x\le b\) zwischen dem Graphen von \(h\) und der x-Achse liegt. - Dem Graphen von \(h\) ist zu entnehmen, dass der Weckton bestimmte Schalldruckpegel mehr als einmal annimmt. Zwei Zeitpunkte mit gleichem Schalldruckpegel haben jeweils einen bestimmten Abstand. Bestimme rechnerisch den größten dieser Abstände.
| AFB II, III - K1 K2 K3 K4 K5 K6 | Quelle IQB e.V. | #iqb |
8 Hängebrücke (k.A.) 𝕃
Die Abbildung 1 zeigt schematisch die achsensymmetrische Seitenansicht einer Hängebrücke. Die beiden vertikalen Pfeiler haben einen Abstand von 400 m. Die Wasseroberfläche liegt 20 m unterhalt der Fahrbahn.
Die beiden Pfeiler gliedern die Brücke in einen linken, einen mittleren und einen rechten Abschnitt. Am oberen Ende jedes Pfeilers ist sowohl das Tragseil des mittleren Abschnitts als auch das Abspannseil des linken bzw. rechten Abschnitts befestigt. Die beiden Abspannseile sind am jeweiligen Ende der Fahrbahn verankert.
Im verwendeten Koordinatensystem entspricht eine Längeneinheit 10 m in der Realität.
In der Seitenansicht der Brücke verläuft die x-Achse entlang der horizontal verlaufenden Fahrbahn, die y-Achse entlang der Symmetrieachse.
- Im rechten Abschnitt der Brücke wird der Verlauf des Abspannseils modellhaft durch
den Funktionsterm \(r(x)=\frac{253}{100}\cdot \left(e^{\frac{1}{11}\cdot (32-x)}-1 \right)\) beschrieben.- Zeige, dass die Fahrbahn der Brücke insgesamt 640 m lang ist.
- Auch im linken Abschnitt der Brücke kann der Verlauf des Abspannseils im Modell durch einen Funktionsterm beschrieben werden. Gib einen passenden Term \(l(x)\) sowie das Intervall an, in dem dieser Term das Abspannseil darstellt.
- Berechne die Höhe der Pfeiler über der Wasseroberfläche.
- Berechne die Größe des Winkels, unter dem das rechte Abspannseil auf den zugehörigen Pfeiler trifft
- In der Seitenansicht begrenzen der rechte Pfeiler, das zugehörige Abspannseil und die Fahrbahn ein Flächenstück. Berechne dessen Inhalt in der Realität.
- Im Folgenden wird der mittlere Abschnitt der Brücke betrachtet. Die vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Man hat sowohl von den Pfeilern als auch untereinander einen horizontalen Abstand von 16 m.
Der Verlauf des Tragseils wird modellhaft durch den Funktionsterm \(s(x)=\left(\frac{1}{8}\right)^6\cdot \left(x^4+2560x^2\right)+\frac{125}{256}\) beschrieben.- Begründe, dass der Term von \(s\) damit in Einklang steht, dass die Seitenansicht der Brücke achsensymmetrisch ist.
- Zwei Punkte des Tragseils in der rechten Hälfte des mittleren Abschnitts haben einen horizontalen Abstand von 40 m und einen Höhenunterschied von 5 m. Gib eine Gleichung an, deren Lösung die x-Koordinate des höher liegenden Punkts im Modell ist.
- Gib die Bedeutung des Terms \(\left(\sum\limits_{k=1}^{24}s(-20+1,6\cdot k)\right)\cdot 10\) im Sachzusammenhang an und begründe deine Angabe.
- Die Lösung der Gleichung \(\frac{s(x)-0}{x-20}\cdot s^\prime(x)=-1\)ermöglicht die Berechnung eines Abstands im Sachzusammenhang. Gib an, um welchen Abstand es sich handelt, und begründe deine Angabe.
Der Verlauf des Tragseils kann näherungsweise durch einen Kreisbogen beschrieben werden. Dazu dient der Kreis mit dem Mittelpunkt \(M\left(0|\frac{1699}{36}\right)\), der durch die Punkte \(A\left(-20|5\right), B\left(20|5\right) \ \text{und} \ C\left(0|\frac{1}{2}\right)\) verläuft (vgl. Abbildung 2). Berechne unter Verwendung des Kreisbogens die Länge des Tragseils.
| AFB I, II, III - K1 K2 K3 K4 K5 K6 | Quelle IQB e.V. | #iqb |
9 Sinusgraph (k.A.) 𝕋 𝕃
Die Abbildung zeigt den Graphen \(G_f\) der in \(\mathbb{R}\) definierten Funktion \(f\) mit \(f\left(x\right)=2\cdot\sin{\left(\frac{1}{2}x\right)}\).
- Beurteile mithilfe der Abbildung, ob der Wert des Integrals \(\int_{-2}^{8}{f\left(x\right)\mathrm{d} x}\) negativ ist.
- Weise nach, dass folgende Aussage zutrifft:
Die Tangente an \(G_f\) im Koordinatenursprung ist die Gerade durch die Punkte \(\left(-1\middle|-1\right)\) und \(\left(1\middle|1\right)\).
| AFB k.A. - K1 K2 K4 K5 | Quelle IQB e.V. | #iqb |
10 Grafisch Integralwert bestimmen (k.A.) 𝕋 𝕃
Die Abbildung zeigt den Graphen \(G_f\) einer in \(\mathbb{R}\) definierten Funktion \(f\).
- Bestimme grafisch den Wert des Integrals
\(\int\limits_{-3}^{-1,5}{f\left(x\right)\mathrm{d} x}\) - Beschreibe, wie der Graph der in \(\mathbb{R}\) definierten Funktion \(u\)mit \(u\left(x\right)=-f\left(x\right)+2\) aus \(G_f\) erzeugt werden kann. Gib die Koordinaten des Hochpunkts des Graphen von \(u\) an.
| AFB k.A. - K2 K4 K6 | Quelle IQB e.V. | #iqb |
