Zum Inhalt springen

BPE 13 Einheitsübergreifend

Version 12.1 von akukin am 2024/03/07 16:55
Inhalt

Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit p(x)=x^q;\: x\neq 0.

Für b \rightarrow \infty heißt U_q=\int_1^b{p(x)}\cdot dx uneigentliches Integral über p, falls U_q eine reelle Zahl ergibt.

Überprüfe, für welche Werte von q das uneigentliche Integral U_q existiert.

x hoch minus 2.png

#problemlösen

AFB   IIIKompetenzen   K2 K5Bearbeitungszeit   40 min
Quelle   Dr. Andreas DinhLizenz   CC BY-SA

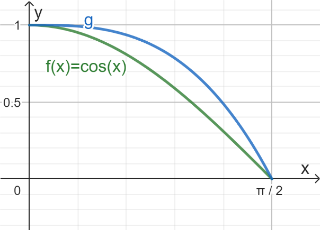cos und pot.pngIn [0; \pi/2] soll die Funktion f mit f(x)=\cos{x} durch eine Potenzfunktion g mit g(x)=1-ax^q angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.

  1. Bestimme a in Abhängigkeit von q.

  2. Begründe, weshalb ein kleiner Wert des Integrals

    \int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx

    ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.

  3. Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.

(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)

#problemlösen

AFB   IIIKompetenzen   K2 K5 K4Bearbeitungszeit   30 min
Quelle   Dr. Andreas DinhLizenz   CC BY-SA

GraphSteigungVolumen.PNG
Die Abbildung zeigt den Graphen einer in \mathbb{R} definierten Funktion f.

  1. Beurteile die folgende Aussage:
    Für jeden Wert von x mit 0\leq x\leq 2 ist die Steigung des Graphen von f kleiner als 3.
  2. Mit dem Term \pi\cdot\int\limits_{0}^{2}{\left(f\left(x\right)\right)^2\mathrm{d} x}
    kann das Volumen eines Körpers berechnet werden.
    Begründe, dass dieses Volumen größer als \pi\cdot{0,5}^2+\pi\cdot1^2 ist.

#iqb

AFB   k.A.Kompetenzen   K1 K2 K4 K5 K6Bearbeitungszeit   k.A.
Quelle   IQBLizenz   k.A.

Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau.
An einem bestimmten Tag entsteht der Stau um 06:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge mithilfe der in \mathbb{R} definierten Funktion f mit f\left(x\right)=x\cdot\left(8-5x\right)\cdot\left(1-\frac{x}{4}\right)^2 beschrieben werden. Dabei gibt x die nach 06:00 Uhr vergangene Zeit in Stunden und f\left(x\right) die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.

  1. Nenne die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründe anhand der Struktur des Funktionsterms von f, dass es keine weiteren solchen Zeitpunkte gibt.
  2. Es gilt f\left(2\right)<0. Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
  3. Bestimme den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt. Zeige, dass der zugehörige Wert der momentanen Änderungsrate zwischen 2 km/h und 3 km/h liegt.
  4. Gib den Zeitpunkt an, zu dem der Stau am längsten ist. Begründe deine Angabe.

Im Sachzusammenhang ist neben der Funktion f die in \mathbb{R} definierte Funktion s mit s\left(x\right)=\left(\frac{x}{4}\right)^2\cdot\left(4-x\right)^3 von Bedeutung.

  1. Begründe, dass die folgende Aussage richtig ist:
    Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion s angegeben werden.
    Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat.
  2. Berechne die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimmen Sie für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge.
  3. Bestimme denjenigen Zeitpunkt zwischen 06:00 Uhr und 10:00 Uhr, zu dem
     die Staulänge 0,5 km geringer ist als eine Stunde vorher.
  4. Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 1 gezeigten Graphen dargestellt. Dabei ist x die nach 06:00 Uhr vergangene Zeit in Stunden und y die momentane Änderungsrate der Staulänge in Kilometer pro Stunde.
    Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat. Markieren Sie diesen Zeitpunkt in der Abbildung 1, begründe dein Markierung und veranschauliche deine Begründung in der Abbildung 1.

#iqb

AFB   I, II, IIIKompetenzen   K1 K2 K3 K4 K5 K6Bearbeitungszeit   k.A.
Quelle   IQBLizenz   k.A.

Kompetenzmatrix und Seitenreflexion

K1K2K3K4K5K6
I000000
II000000
III020120
Bearbeitungszeit gesamt: 70 min
Abdeckung Bildungsplan
Abdeckung Kompetenzen
Abdeckung Anforderungsbereiche
Eignung gemäß Kriterien
Umfang gemäß Mengengerüst