1 Skate-Rampe (k.A.) 𝕃
Die folgende Abbildung zeigt eine Skate-Rampe.
Abb.: Skate-Rampe (vgl. Haas & Morath (2006) (Hrsg.). „Anwendungsorientierte Aufgaben für die Sekundarstufe II“(S.39). Braunschweig: Westermann Verlag.)
Die Rampe ist massiv aus Beton gegossen. Diskutiere Möglichkeiten, das Gewicht der Rampe nur anhand der Abbildung und der Dichte von Beton (zwischen 1,5 und 2,5 g/cm3) abzuschätzen.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB k.A. - k.A. | Quelle Problemlösegruppe | #problemlösen |
2 Spielzeug-Holzbrücke Symmetrie (k.A.) 𝕃
Die Abbildung zeigt modellhaft den Längsschnitt einer dreiteiligen Brücke aus Holz für eine Spielzeugeisenbahn. Die Züge können sowohl über die Brücke fahren als auch darunter hindurch.
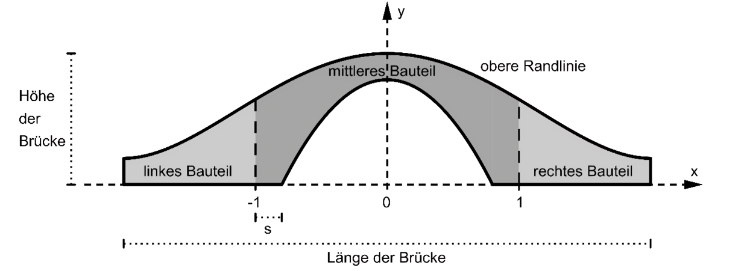
Die obere Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen der in \(\mathbb{R}\)definierten Funktion \(f: x \mapsto \frac{1}{20} x^4-\frac{2}{5}x^2+1\) beschrieben werden. Dabei werden die Endpunkte dieser Randlinie durch die beiden Tiefpunkte des Graphen von \(f\) dargestellt. Im verwendeten Koordinatensystem beschreibt die x-Achse die Horizontale; eine Längeneinheit entspricht einem Dezimeter in der Realität.
Während der Planung der Brückenform kamen zur Beschreibung der oberen Randlinie für das linke Bauteil eine Funktion \(g_l\) und für das rechte Bauteil eine Funktion \(g_r\) infrage. Auch bei Verwendung dieser Funktionen wäre die obere Randlinie achsensymmetrisch gewesen.
- Beurteile jede der folgenden Aussagen:
I: \(-g_l(x)=g_r(-x)\) für \(-2\leq x \leq -1\)
II: \(g_l(x-1)=g_r(-x+1)\) für \(-1\leq x\leq 0\)
Die Form und die Größe der Brücke werden verändert, indem im bisher verwendeten Modell die obere Randlinie des Längsschnitts mithilfe der in \(\mathbb{R}\)definierten Funktion \(k:x\mapsto\frac{3}{5} \cdot \cos(\frac{\pi}{3}x)+\frac{4}{5}\) beschrieben wird. Die Bauteile der veränderten Brücke lassen sich nach dem in der folgenden Abbildung dargestellten Prinzip aus einem quaderförmigen Holzblock sägen. Der beim Sägen auftretende Materialverlust soll im Folgenden vernachlässigt werden.

- Der Graph von \(k\) ist symmetrisch bezüglich jedes seiner Wendepunkte. Beschreibe, wie diese Eigenschaft mit dem in der 2. Abbildung dargestellten Prinzip zusammenhängt.
- Ermittle mithilfe des Funktionsterms von \(k\) den Flächeninhalt der gesamten in der 2. Abbildung gezeigten rechteckigen Vorderseite des Holzblocks.
| AFB III - K1 K3 K4 K6 | Quelle IQB | #iqb ))) |
3 CO2-Konzentration trigonometrisch (k.A.)
In einer Messstation wird seit 1958 kontinuierlich die CO2-Konzentration in der Luft
gemessen, die in ppm (parts per million) angegeben wird. Innerhalb eines Jahres schwankt die CO2-Konzentration. Für einen bestimmten Zeitraum von acht Monaten lassen sich die gemessenen Werte modellhaft durch die in \(\mathbb{R}\) definierte Funktion \(k: x \mapsto 3,3\cdot \sin\left(\frac{\pi}{6}x\right)+406\) beschreiben. Dabei ist \(x\) die in diesem Zeitraum vergangene Zeit in Monaten und \(k(x)\) die CO2-Konzentration in ppm. Vereinfachend wird davon ausgegangen, dass jeder Monat 30 Tage hat.
- Gib an, wie der Graph von \(k\) schrittweise aus dem Graphen der in \(\mathbb{R}\) definierten Funktion \(s: x \mapsto \sin(x)\) hervorgeht. Beurteile, ob die Reihenfolge der einzelnen Schritte von Bedeutung ist.
| AFB II - K1 K4 K6 | Quelle IQB | #iqb |
4 Anzahl Gleichungslösungen (k.A.)
Gegeben sind die in \(\mathbb{R}\) definierten Funktionen \( f: x \mapsto \cos(x)\) und \( g_k: x \mapsto k\cdot x^2\) mit \( k \in \mathbb{R}^+\). Die Abbildung zeigt die Graphen von \(f\) und \(g_{\frac{1}{50}}\).
1.Entscheide, ob es Werte von \(k\) gibt, für die die Gleichung \(f(x)=g_k(x)\) mehr als 2022 Lösungen hat. Begründe deine Entscheidung.
| AFB k.A. - K1 K6 | Quelle IQB | #iqb |
IQB-Index
BPE 1
Abstand Graph Koordinatenursprung
BPE 4
Aufstellen eines Funktionstermes, CO2-Konzentration, Radioaktiver Zerfall
BPE 7
Eckpunkte einer Pyramide, Pyramide, Gleichschenkliges Dreieck, Saarpolygon, Zylinder, Vektoren Sechseck, Nachweis Dreieck, Flächeninhalte Verhältnis, Punktbestimmung durch Skalarprodukt, Nachweis Quader, Berechnungen am Quader, Rasenfläche, Gleichschenkliges Dreieck und Flächeninhalt, Ähnlichkeit und Strahlensätze, Dreieck Koordinaten, Parallelogramm
BPE 10
Sinusparameter bestimmen, Kosinusfunktion aufstellen, Anzahl Gleichungslösungen, CO2-Konzentration trigonometrisch
BPE 12
Verschiebung durch Ableiten, Ableitung berechnen und grafisch ermitteln, Verschiebung durch Ableiten, Transformation, Stammfunktion, Tangente und Schnittpunkt, Grad, Skizze, Kosinusfunktion, Periode, Steigung, Lokale und mittlere Änderungsrate
BPE 13
Fläche, Quadrat, Funktionsschar, Symmetrie und Flächeninhalt, Steigung, Volumen, Stau MMS, Stau WTR, Schalldruck1, Schalldruck2, Hängebrücke, Sinusgraph, Grafisch Integralwert bestimmen
BPE 16
Geradenschar, LGS graphisch, Doppelpyramide, Gleichschenkliges Dreieck und Flächeninhalt, Raute, Geradenschar, Rechtwinklig-gleichschenkliges Dreieck, Spiegelebene, Rasenfläche, Ebenenschar, Oktaeder, Geraden zeichnen, Quader verschieben, Geradenlage und rechter Winkel, Quadrat Diagonale
BPE 17
Zwei Behälter, Glücksrad, Kugelbehälter, Kugeln mit negativen Zahlen, Zufallsgröße Tetraeder, Glücksrad Zufallsgröße, Würfel beschriften, Glücksrad Spendengala, Verpackter Ball, Dichtefunktion Normalverteilung, Tetraeder, Kugeln und Würfel, Glücksradiqb, Urlaubsreise, Olivenöl
