Index Problemlösen
Unten auf der Seite gibt es Links zu Teilheften mit Problemlöseaufgaben.
BPE 1
Erkunden unbekannte Funktionsgleichung, Pythagoreisches Tripel, Arithmagon Darstellungsformen, Gitterpunkte, Verbindungsstrecken von Eckpunkten, Fussball
BPE 2
Venn - Eigenschaften, Arithmagon Darstellungsformen, Füllstände
BPE 3
Arithmagon Darstellungsformen, Parabelmaschine, Open Middle, Nichomachus
BPE 5
Quadrat in Kreis, Unendliche Quadrate, Blättchen, Quadrat-Spirale, Pilot, Ameise, Gemeinsame Tangenten, Die Rätsel um Johannes und Wilhelm, Gaußsche Summenformel
BPE 8
Lichtschalterproblem, Türme von Hanoi, Kreismittelpunkt
BPE 10
Zwei Funktionen mit gemeinsamen Punkten
BPE 12
Aufleiten ln, Funktion gesucht, Monotonie, L’Hospital
BPE 13
Integralfunktion, Uneigentliches Integral, Annäherung
BPE 14
Funktionsterme aus Eigenschaften
BPE 17
Grashalme, Nüsse, Kugeln hinzufügen, Raucher, Stochastische Unabhängigkeit Wahrscheinlichkeiten, Kombinatorik, Glücksrad
Eingangklasse
Jahrgangsstufen
BPE 17.3 Baumdiagramm, Vierfeldertafel, Additionssatz und Bedingte Wahrscheinlichkeit
Aufgabe 40 Raucher 𝕃
Unter den 2500 Mitarbeitern einer Firma sind 1600 Raucher. Von den 2000 Männern rauchen 1400.
Fülle die folgende Tabelle aus und berechne die fehlenden Zellen:
| Raucher | Nichtraucher | ||
|---|---|---|---|
| Frauen | |||
| Männer | |||
Berechne
- den Anteil der Frauen an der Belegschaft,
- den Anteil der Nichtraucher an der Belegschaft,
- wie viel Prozent der Männer rauchen,
- wie viel Prozent der Frauen rauchen
| AFB I | Kompetenzen K3 K4 | Bearbeitungszeit k.A. |
| Quelle Beckstette, Glende, Grasemann, Haasis, Kolupa, Widmann | Lizenz CC BY-SA | |
Eingangklasse
Jahrgangsstufen
BPE 8 Übergreifende Problemlöseaufgaben
Aufgabe 2 Lichtschalterproblem 𝕃
 Ein Hotel hat 100 Zimmer mit den Nummern 1 bis 100 und 100 Gäste. Jedes Zimmer hat einen Lichtschalter, der das Licht einschaltet, wenn es aus ist und es ausschaltet, wenn es an ist.
Ein Hotel hat 100 Zimmer mit den Nummern 1 bis 100 und 100 Gäste. Jedes Zimmer hat einen Lichtschalter, der das Licht einschaltet, wenn es aus ist und es ausschaltet, wenn es an ist.
Zunächst sind alle Lichter ausgeschaltet.
Dann geht jeder Gast der Reihe nach durch jedes Zimmer:
- Gast 1 drückt den Schalter jedes Zimmers.
- Gast 2 drückt den Schalter jedes zweiten Zimmers, also von Zimmer 2, 4, 6, …
- Gast 3 drückt den Schalter jedes dritten Zimmers, also von Zimmer 3, 6, 9, …
- Gast 4…
- …
- Gast 100 drückt den Schalter jedes hundertsten Zimmers, also nur von Zimmer 100.
Beschreibe, wie für ein frei gewähltes Zimmer n (1 ≤ n ≤ 100) geprüft werden kann, ob nach dem Durchgang des letzten Gastes das Licht aus- oder eingeschaltet ist.
(Bonus: Simuliere das Lichtschalter-Problem mit einer Tabellenkalkulation oder mithilfe einer Programmiersprache und überprüfe, welche Lichter nach dem kompletten Durchlauf aus sind. (30min, AB II für Bonus-Aufgabe))
Bild: 4028mdk09, Lichtschalter mechanisch, CC BY-SA 3.0
| AFB II | Kompetenzen K2 K1 K6 K5 | Bearbeitungszeit 20 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 2 Türme von Hanoi 𝕃
 Die „Türme von Hanoi“ sind ein altes asiatisches Rätselspiel, welches im 19. Jahrhundert im Westen eingeführt wurde.
Die „Türme von Hanoi“ sind ein altes asiatisches Rätselspiel, welches im 19. Jahrhundert im Westen eingeführt wurde.
Es besteht aus drei am Boden fixierten senkrechten Stäben, von denen zu Beginn die rechte und mittlere Stange unbelegt sind und die linke Stange eine n-stöckige Pyramide enthält, deren Stöcke aus gelochten Scheiben abnehmender Größe besteht. Die Abbildung rechts zeigt eine Holzversion des Spiels mit n=8 Stöcken.
Ziel des Spiels ist, die komplette Pyramide in möglichst wenigen Zügen auf den rechten Stab zu versetzen. Pro Zug darf genau eine Scheibe von einem Stab oben abgezogen und auf einen anderen Stab gesetzt werden. Dabei darf niemals eine Scheibe auf eine kleinere Scheibe abgelegt werden.
Untersuche in Abhängigkeit von n, in wie vielen Zügen N das Spiel optimalerweise gelöst werden kann.
Bild: anonym, Tower of Hanoi, CC BY-SA 3.0
| AFB II | Kompetenzen K2 K4 K5 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
BPE 10.4 Aufstellen von Funktionstermen
Aufgabe 7 Zwei Funktionen mit gemeinsamen Punkten 𝕃
Auf dem Intervall \(]0;6[ \) sollen zwei trigonometrische Funktionen genau fünf gemeinsame Punkte besitzen.
Bestimme zwei mögliche Funktionsterme, für die dies zutrifft. Überprüfe dein Ergebnis.
| AFB II | Kompetenzen K2 | Bearbeitungszeit 15 min |
| Quelle Ingrid Kolupa, Katharina Justice | Lizenz CC BY-SA | |
BPE 12.7 Monotonie
Aufgabe 21 Monotonie 𝕃
f bezeichnet im Folgenden eine im ganzen Definitionsbereich D knickfreie Funktion.
Streng steigende Monotonie ist für f wie folgt definiert:
Wenn für alle \(a, b \in \textbf{D}\) mit \(a<b\) gilt: \(f(a)<f(b)\), heißt f streng monoton steigend.
Aus dem Unterricht wissen wir, dass wir streng steigende Monotonie auch wie folgt untersuchen können:
Wenn für alle \(x \in \textbf{D}\) gilt: \(f'(x)>0\), dann ist f streng monoton steigend.
Zeige mit Hilfe einer geeigneten Funktion f folgende Aussage:
Eine Funktion kann auch dann streng monoton steigend sein, wenn \(f'(x)>0\) nicht für alle \(x \in \textbf{D}\) gilt.
| AFB II | Kompetenzen K1 K2 K5 | Bearbeitungszeit 25 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
BPE 14.1 Aufstellen von Funktionstermen
Aufgabe 28 Funktionsterme aus Eigenschaften 𝕃
Gegeben sind die folgenden Eigenschaften einer Funktion:
- \(f(2)=f(4)\)
- \(f^{\prime}(3)= 0\)
- \(f^{\prime}(2)\approx 4,7\)
- \[\int\limits_{0}^4 f(x)dx \geq \int\limits_{0}^1 f(x)dx > \int\limits_{0}^2 f(x)dx\]
Bestimme einen Funktionsterm, der alle vier Bedingungen erfüllt.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen K2 K5 K4 | Bearbeitungszeit 20 min |
| Quelle Problemlösegruppe | Lizenz CC BY-SA | |
BPE 17.1 Zufallsexperimente, Häufigkeit und Wahrscheinlichkeit
Aufgabe 38 Grashalme 𝕃
Ausgangspunkt: Wenn früher in Russland eine junge Frau wissen wollte, ob sie im nächsten Jahr verheiratet sein werde, fragte sie das Grashalm-Orakel: Sie nahm mehrere Paare langer Grashalme in die Faust, so dass sie oben und unten herausragten, und bat eine Freundin, alle Enden oberhalb der Faust irgendwie zufällig, aber paarweise, zusammenzuknoten. Bei allen Enden unterhalb der Faust ebenso. Dann öffnet das Mädchen die Faust.
Falls dabei ein einziger großer Ring aus Gras entsteht, bedeutet dies, dass die junge Frau im nächsten Jahr heiraten werde.
Begründe, dass die Wahrscheinlichkeit bei 2 Paaren, also 4 Grashalmen, durch \(P = \frac{4}{5}\cdot \frac{2}{3}= \frac{8}{15} \approx 53,3 \%\) berechnet werden kann. Berechne damit die Wahrscheinlichkeit, dass bei 3 Paaren, also 6 Grashalmen, ein einziger Ring entsteht.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen K1 K6 K4 | Bearbeitungszeit k.A. |
| Quelle Stefan Rosner | Lizenz CC BY-SA | |
Aufgabe 40 Nüsse 𝕃
Vor vielen Jahren, als es noch keine Handyspiele gab, spielte man in der Weihnachtszeit beim Nüsse-Essen mit den Nussschalen.
Halbe Nussschalen wurden geworfen und bleiben so ◡ oder so ◠ liegen. Man hat immer zwei halbe Schalen geworfen.
Zwei Nussschalen liegen ◡ ◡ oder ◠ ◠ oder eine ◡ und die andere ◠.
Der Fall ◠ ◠ kam am seltensten vor. Aber die beiden anderen Fälle ( ◡ ◡ und verschiedene Lage) waren etwa gleich häufig.
Berechne die Wahrscheinlichkeit, dass eine halbe Nussschale in die Lage ◡ fällt.
| AFB II | Kompetenzen K2 K3 K5 | Bearbeitungszeit k.A. |
| Quelle Helmut Diehl, Frenzen | Lizenz CC BY-SA | |
Aufgabe 49 Glücksrad 𝕃
Ein Glücksrad mit einem roten Gewinnbereich von einem Viertel wird so gedreht, dass es in einer völlig zufälligen Position zum Stillstand kommt. Einen Beobachter interessiert, wie groß der Abstand der Halteposition (grünes Dreieck in der Skizze) zum Gewinnbereich ist. Er misst den Abstand in Grad.
So ist der Abstand z.B. 0°, falls das Glücksrad im Gewinnbereich zum Stillstand kommt und 90°, falls es nach einem Drittel oder zwei Dritteln des Verlustbereichs zum Stillstand kommt.
Bestimme mit Hilfe einer geeigneten Zeichnung den Erwartungswert dieses Abstands bei einmaliger Drehung des Glücksrads.
| AFB II | Kompetenzen K2 K4 K5 | Bearbeitungszeit 20 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Eingangklasse
Jahrgangsstufen
BPE 8 Übergreifende Problemlöseaufgaben
Aufgabe 2 Kreismittelpunkt 𝕃
Gegeben ist ein Kreis. Auf diesem werden zufällig drei Punkte A, B und C ausgewählt und durch ein Dreieck miteinander verbunden.
Mit welcher Wahrscheinlichkeit liegt der Mittelpunkt des Kreises innerhalb des Dreiecks (oder auf einer Dreiecksseite)?
| AFB III | Kompetenzen K2 K4 K5 K6 | Bearbeitungszeit 20 min |
| Quelle Stefan Rosner | Lizenz CC BY-SA | |
BPE 12.4 Stammfunktionen, Graphisches Aufleiten
Aufgabe 18 Aufleiten ln (eAN) 𝕃
Im Unterricht eines J2-Kurses soll die Funktion \(f(x)=\frac{1}{2x}\) aufgeleitet werden. Johann rechnet mit der Kettenregel der Aufleitung wie folgt: \(F(x)=\frac{1}{2}\ln(|2x|)\). Johannes mag die Kettenregel nicht und formt den Term von f zunächst um: \(f(x)=\frac{1}{2}\cdot\frac{1}{x}\), denn danach wird die Aufleitung ganz einfach: \(F(x)=\frac{1}{2}\ln(|x|)\). Die beiden geraten in eine Diskussion darüber, welche Lösung richtig ist. Überprüfe dies.
| AFB III | Kompetenzen K5 | Bearbeitungszeit 15 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 19 Funktion gesucht 𝕃
Bestimme einen Funktionsterm, dessen Graph an der Stelle x = 2 die Tangente \(g(x)=\frac12 x+1\) hat.
| AFB III | Kompetenzen K2 K5 | Bearbeitungszeit 11 min |
| Quelle Holger Engels | Lizenz k.A. | |
Aufgabe 23 L’Hospital (M+) 𝕃
Im Zusammenhang mit Exponentialfunktionen hast du von deinem Lehrer vielleicht erfahren, dass jede beliebige Exponentialfunktion f mit \( f(x)=a\cdot q^x + b, x \in \mathbb{R}, a,b \in \mathbb{R}, q \in \mathbb{Q}, \) „schneller wächst“ als jede beliebige Potenzfunktion g mit \( g(x)= \tilde{a} \cdot x^r + \tilde{b}, x \in \mathbb{R}, \tilde{a},\tilde{b} \in \mathbb{R}, r \in \mathbb{Q} \).
Gemeint ist mit dieser Formulierung: Ab einem bestimmten \(x\)-Wert \(x_0 \) ist \( f(x)>g(x) \) für alle \(x>x_0 \).
Betrachtet man z. B. die Funktionen \( f(x) = \frac{1}{30} \cdot 1,01^x\) und \( g(x)= x^{100} \), so scheint dies nicht der Fall zu sein (vgl. Abbildung).
Untersuche, ob Exponentialfunktionen tatsächlich immer „schneller wachsen“ als Potenzfunktionen.
Verwende hierfür ein- oder mehrmalig die Regel von de L’Hospital, die für zwei ableitbare Funktionen f und g Folgendes besagt:
(Die Regel setzt man ein, wenn für \( x \rightarrow \infty\) Zähler und Nenner beide gegen 0 oder beide gegen \(-\infty\) oder, wie im Fall dieser Aufgabe, beide gegen \(+\infty \) gehen.)
Für die Aufgabe nicht benötigte Zusatzbemerkung: Die Regel gilt auch für \( x \rightarrow -\infty\) und für \( x \rightarrow x_0, x_0 \in \mathbb{R}\).
| AFB III | Kompetenzen K2 K4 K5 K6 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
BPE 13.2 Hauptsatz der Differenzial- und Integralrechnung, Bestimmtes Integral
Aufgabe 25 Integralfunktion 𝕃
Paul, Sevda und Lucie wiederholen die Integralfunktion. Sie haben verstanden, dass jede Integralfunktion \(I_a\) einer Funktion f auch Stammfunktion derselben Funktion f ist. In der Lerngruppe herrscht nun jedoch Uneinigkeit darüber, ob umgekehrt jede Stammfunktion auch Integralfunktion ist.
- Paul behauptet, dies sei für jede Funktion f der Fall.
- Sevda meint dagegen, jede Funktion besäße auch Stammfunktionen, die keine Integralfunktionen sind.
- Lucie zuletzt ist der Auffassung, dass es von der Funktion abhänge.
Begründe zunächst, weshalb jede Integralfunktion von f auch Stammfunktion von f ist. Überprüfe dann, wer Recht hat.
| AFB III | Kompetenzen K2 K1 K5 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 27 Uneigentliches Integral (M+) 𝕃
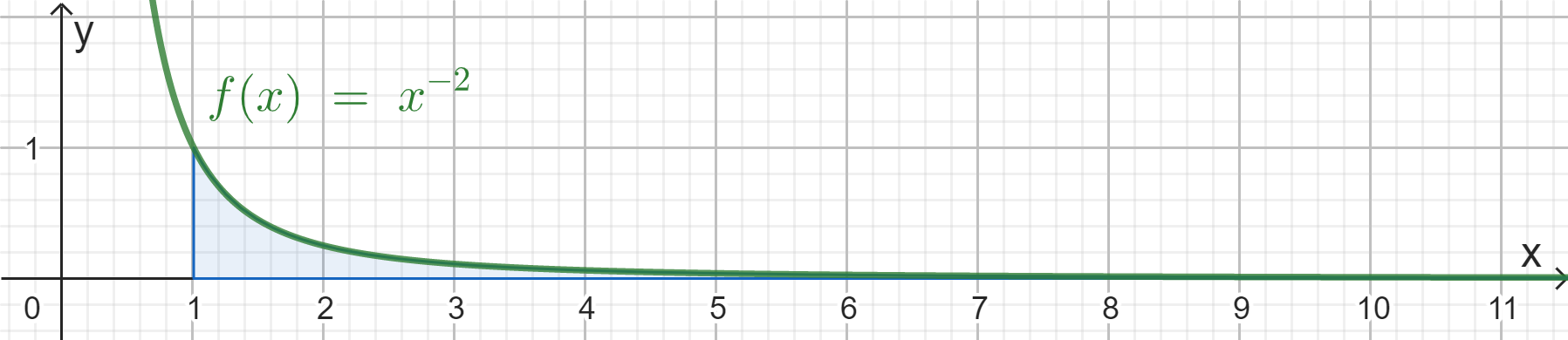
Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit \(p(x)=x^q;\: x\neq 0\).
Für \(b \rightarrow \infty\) heißt \(U_q=\int_1^b{p(x)}\cdot dx\) uneigentliches Integral über p, falls \(U_q\) eine reelle Zahl ergibt.
Überprüfe, für welche Werte von q das uneigentliche Integral \(U_q\) existiert.
| AFB III | Kompetenzen K2 K5 | Bearbeitungszeit 40 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 27 Annäherung 𝕃
 In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
- Bestimme a in Abhängigkeit von q.
Begründe, weshalb ein kleiner Wert des Integrals
\[\int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx\]ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.
- Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.
(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)
| AFB III | Kompetenzen K2 K5 K4 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
BPE 17.3 Baumdiagramm, Vierfeldertafel, Additionssatz und Bedingte Wahrscheinlichkeit
Aufgabe 40 Kugeln hinzufügen 𝕃
In einer Schüssel sind 20 rote und 10 gelbe Kugeln. Es werden mit einem Zug zwei Kugeln gezogen.
Wie viele blaue Kugeln müssen dazugegeben werden, damit die Wahrscheinlichkeit, zwei gleichfarbige Kugeln zu bekommen,
a) genau \(\frac{70}{183}\) ist? b) höchstens 0,4 ist? c) mindestens 0,5 ist?
| AFB III | Kompetenzen K2 K5 | Bearbeitungszeit k.A. |
| Quelle Beckstette, Glende, Grasemann, Haasis, Kolupa, Widmann | Lizenz CC BY-SA | |
Aufgabe 40 Stochastische Unabhängigkeit Wahrscheinlichkeiten 𝕃
In einer Urne befinden sich 14 durchnummerierte Kugeln. Eine Kugel wird zufällig gezogen. Die Ergebnismenge ist \(\Omega = \lbrace 1, 2, 3, ..., 12, 13, 14 \rbrace \).
- Gib ein Ereignis E an mit Wahrscheinlichkeit \(P(E)=\frac{1}{7}\).
- Begründe, warum zwei Ereignisse F und G mit \(P(F)=P(G)=0{,}8\) stets stochastisch abhängig sind.
| AFB III | Kompetenzen K2 K4 K5 | Bearbeitungszeit k.A. |
| Quelle Niklas Wunder | Lizenz CC BY-SA | |
Aufgabe 41 Kombinatorik 𝕃
 Fünf zehnseitige Würfel (mit den Zahlen 1–10) werden gleichzeitig in einem Würfelbecher geworfen. Für jeden Würfel beträgt die Wahrscheinlichkeit für jede Augenzahl 10%.
Fünf zehnseitige Würfel (mit den Zahlen 1–10) werden gleichzeitig in einem Würfelbecher geworfen. Für jeden Würfel beträgt die Wahrscheinlichkeit für jede Augenzahl 10%.
Untersuche, wie viele unterschiedliche Wurfbilder geworfen werden können. (unterschiedlich im Sinne von alle verschieden, zwei gleiche, ..., alle gleich)
Bild: Dietmar Rabich, Würfel, pentagonales Trapezoeder, Ausschnitt, CC BY-SA 4.0
| AFB III | Kompetenzen K2 K5 K6 | Bearbeitungszeit 25 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
